| designation: | D1-001 |
|---|---|
| author: | andrew white |
| status: | under observation |
| prepared date: | september 30, 2024 |
| updated date: | October 5, 2024 |
abstract: I'm sick of people drawing plots that show intelligence going upwards forever. There are limits on how much compute can be applied and so I've made few short arguments on what are upper limits on these kind of plots.
the upper limit of intelligence
I keep seeing plots like this:
There are some upper limits on this though - you cannot just scale indefinitely. All exponential processes end - from COVID-19 to listener growth on your podcast.
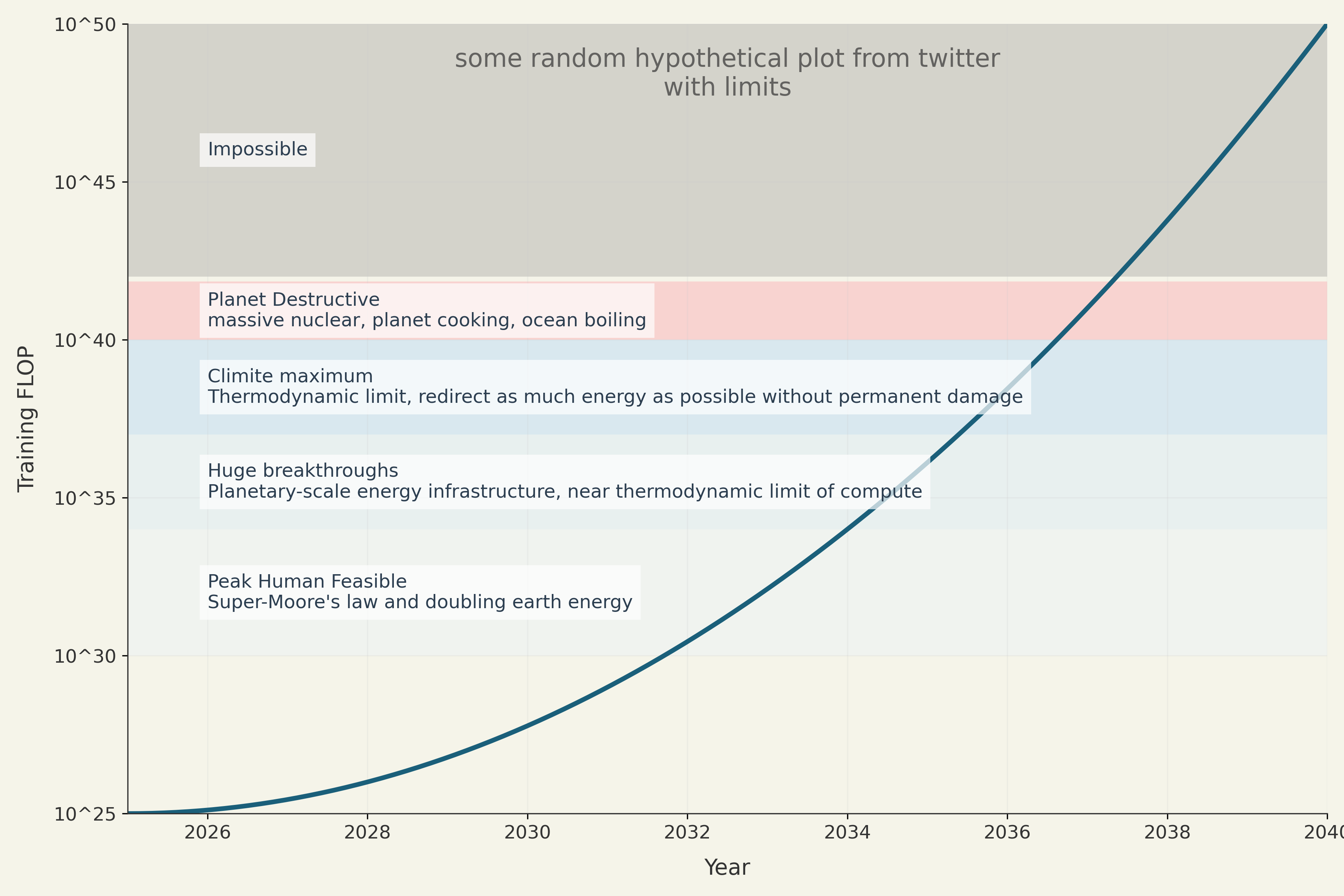
Here I make some arguments about an upper limit of trained AI systems based on resources, physics, and thermodynamics of compute. That limit, without planet-scale upheaval, is about GPT-9 level ( FLOP). If there are no concerns for the ecosystem or climate on Earth, a GPT-11 scale system could be trained ( FLOP). If a massive fleet of nuclear reactors is built at a scale large enough to raise the temperature of Earth by 35 degrees C and destroy the climate, then GPT-11.5 could be built. These are the upper bounds for a hypothetical terrestrial superintelligence.
So plots should look like
factors
Here's what I'll consider:
- energy: bounded by solar radiation on Earth and heat dissipation of plant. Key limiter of compute
- compute: bounded by thermodynamics and tightly coupled with intelligence. Key limiter of intelligence
- models: used to estimate intelligence output from compute input
energy
Let's consider a few scenarios on a scale of increasing energy: to :
- GW ( W) - the current energy capacity of datacenters in US1
- TW ( W) - the scale of current global energy production
- PW ( W) - attainable power by covering most land mass with solar panels2
Nuclear is discussed in more depth below, but the main issue is heat dissipation. Solar doesn't increase the heat dissipation burden on earth from compute, and so is a nice source to draw from in the near term. In practice, the energy generation source doesn't matter for our calculation, but if it exceeds then it will start to run into heat dissipation problems and lead to catastrophic heating of Earth. So is a reasonable upper bound.
calculation:
- Assume: 20% efficiency (from solar panel to compute, very optimistic), 20% of land can be practically covered by solar.
- Given: Earth is m, Energy absorbance is 168 W / m, land coverage of Earth is 29%
Then:
Adding this many solar panels will lower earth's albedo, leading to less reflectivity of incident light and thus an increase in eath's temperature. However, this effect only will lead to 1-2K of heating.
limits of compute
There are a variety of compute bounds (en.wikipedia.org/wiki/Limits_of_computation). Since we are assuming all our computations will be on Earth, and not some exotic device like a black hole computer or cryogenic computer, the Laundauer Principle will apply because Earth has a finite temperature. Earth's temperature is the result of balancing solar irradiance and radiating heat into space. Using some other form of planetary wide energy would actually increase the temperature, so solar has an advantage there. Since we're not inserting new energy into Earth, the temperature is unlikely to deviate much the current average 290K.
Landauer's principle is an experimentally verified compute bound3 that states erasing one bit of information in a computational process requires a minimum amount of energy:
At 300K4, the minimum energy per bit operation is:
This is the heat we must dissipate per operation. Let us assume that our processor is at equilibrium: all heat that goes into the processor is dissipated because of the conservation of energy. Then is equal to the amount of energy that must be delivered per operation.
To convert to floating point operations, I'll assume about 50 bit operations per FLOP. This number is a bit tricky, because it depends on precision, specific operations, and the Landauer principle only applies to operations that erase bits. This gives our limit for FLOPS / W as:
This is equivalent to running a current frontier datacenter on a single watt.5 Today's numbers for current phones/GPUs are about to FLOPS / W. Humans compute on about 20 W (2,000 calories per day, 20% to the brain). Assuming Moore's law-like improvements on efficiency, this is about 30 years of progress. This means that even with unlimited intelligence, this is the upper limit on (terrestrial) compute efficiency from thermodynamics.
Let's consider the following scenarios:
- : current best case compute efficiency
- : 1% of Laundauer Principle limit is attainable
- : ~100% of Laundauer Principle limit is attainable
This gives us a few plausible compute scenarios from contemporary, reasonable, and to the boundary of thermodynamics.
models
We will assume the current paradigm for training frontier LLMs models: an expensive long-running training job, followed by negligible cost on inference.6 The current estimate for GPT-4 training compute is FLOP.7 If we use past GPT model steps as a measure, then GPT-5 should represent about FLOP. Scenario is representative of a national-level megaproject that allocates a significant fraction of GDP to the task and perfect execution/chip availability. Or, a large corporate investment within 5-10 years with projected improvements in compute efficiency and power availability.
- Assume: , , compute efficiency (some account for MFUs/experiments/inference) of 20%
- Given: 6 months of training = seconds
This is a good check on our assessments so far - it matches the assessments from others 8 for 2030 as the expected model size. We might call this GPT-6 (or maybe opus-5) based on extrapolating from current frontier models.
Now let us consider a "runaway recursive improvement" scenario where all intelligence limited tasks are solved and the model training is constructed to be compatible with the current ecosystem on Earth ():
This would be something like GPT-9 in intelligence. It is hard to reason about what an intelligence like this might be capable of. GPT-6 is predicted by some to be artificial general intelligence (AGI), namely roughly equivalent to a human in general capabilities. GPT-9 will be 1,000,000x more capable than GPT-6. The analogy is not perfect, since humans are not good at distributed intelligence, but maybe it will be like having the entire scientific community in each instance of the model and then you can stamp out as many copies of all of human scientists as you would like.
If we now consider a scenario where mass upheaval on earth occurs due to enormous reallocation of resources, covering the world with solar panels, and then finally solving near impossible engineering and physics challenges:
This would be GPT-11.
nuclear
The Earth dissipates heat into space according to the Stefan-Boltzmann Law which is , where is a constant that depends on Earth's emissivity and its surface area. If we use incoming solar to power compute, we do not change the dissipation burden of Earth. That incident sunlight was already coming. However, if we start generating power on earth at a scale similar to incoming solar we will increase Earth's temperature because it will have to dissipate that new heat. This means that switching from solar to nuclear in the calculations above will raise the temperature of Earth which detracts from compute efficiency. Here are some scenarios:
| Nuclear Fraction Relative to | Earth's Temperature |
|---|---|
| 0 | 290K |
| 1x | 291K |
| 10x | 298K |
| 50x | 325K |
Probably 325K is the highest feasible temperature, because that is an average temperature of Earth. You will melt all polar ice and glaciers, raising the ocean height by hundreds of feet. This will release all trapped methane and lead to runaway global warming. You will start boiling fresh water, or even oceans, as the variations of temperature increase. Just kinda bad all around.
In this scenario, our compute efficiency also changes because of the new (optimistic) temperature:
So we get to something like GPT-11.5, but maybe with some downside risk of irreversible destruction of climate.
discussion and limitations
The and scenarios all require distributed training because we are dissipating heat on a planetary scale and that requires maximizing surface area. That surface area forces distribution of compute and then we run into speed of light latency issues, meaning algorithms would need to be developed that handle distributed compute.
There are some technologies that may be relevant that I did not discuss. For example, quantum computing and thermodynamic computing (reversible computing). Quantum computing so far has seemed to excel at relatively narrow tasks, and it's not obvious there will be an unlockable scaling law in quantum computers for general tasks. I guess next token prediction can be reformulated as sampling from an energy distribution and that can be recast as Boson Sampling (which has a quantum advantage). However, it's very much an open question of if quantum will have a meaningful advantage over classical and in some effects it will be the same consequence of reversible computing.
Reversible computing (or thermodynamic computing) is tough for me. It could exceed the Laundauer Principle argument above (like quantum computing would) because it doesn't erase bits. However, it requires new algorithms, hardware, presumably new models, and it is completely unclear if these can exist. It's more unknown than quantum computing. I guess it's feasible that we boot an AI on transformers and the first thing it does is design a new kind of transistor, chips, algorithms, and models to build the next AI on reversible computing.
So quantum computing and reversible computing could move us from the Laundauer Principle argument to the quantum version (Margolus–Levitin) - which will move us to as the compute efficiency limit. I will have to return to this question of dilution refrigerators at the scale of planet compute, but I expect the compute efficiency will not be the bottleneck, but rather moving heat out of the processor while keeping the temperature low.
There are various tricks you can do - like raise the solar panels by 100m to increase surface area. Or, you can create active heat dissipation by launching water or thermal mass into space. Or, maybe stop the rotation of the Earth to concentrate heat on one side of the planet. These either don't provide enough delta to change an order of magnitude or are just so resources intensive themselves that you would be better off moving off of earth.
Ironically, one of the methods to increase the power generation on earth without increasing earth's temperature is to reduce greenhouse gas emissions. Greenhouse gases negatively impact the "atmospheric" window, which controls how much thermal radiation (heat dissipation) earth can emit without being blocked by the atmosphere. Unfortunately, that logic would include oxygen and water vapor as greenhouse gases so that those might need to be scrubbed too from the atmosphere.
Of course you can train for longer than six months, especially once there is no advantage for waiting for chips/power generation to improve. One order of magnitude gain for 5 years - so you could reach GPT-11 () by training for 5,000 years at a "climate compatible" effort. You're probably just better off with starting a Dyson sphere though.
comparison with previous work
I've found this topic to be surprisingly sparse in peer-reviewed literature. There is a paper by Markov in 2014,9 but it focuses on Bremermann compute bounds, which are quite abstract as they are rooted in quantum mechanics and have only been measured in non-classical Margolus–Levitin experiments. That may be feasible at small scales, but if you're doing compute on the scale of planet-wide compute energy then the cooling costs would be infeasible to maintain coherent quantum systems. In cannot be solved via really good insulation, because the Bremermann and Landauer Principle compute analyses are about energy being dissipated from the processor, not being required to provide to the processor. So even if you somehow invent teleportation of energy, you have to couple the system to complex refrigeration to get the heat out and that will cause the energy required to keep those low temperature extremely high (since cooling power removed from the system is proportional to ).
Frank10 has a few nice articles of all the considerations that go into breaking out of the current paradigm to get to reversible computing, but the only real estimates I can find in this work are much more conservative numbers - a limit on conventional computer FLOPS efficiency of , which confusingly is the current approximate efficiency. It is hard to reason about reversible computing to be honest, because it's definition is no change in information (isoentropic/adiabitic) which seems to be at odds with everything we know about intelligence, learning, and model training.
conclusions
GPT-11 ( training FLOP) is an upper limit of achievable training runs that are compatible with earth's temperature, solar radiation, heat dissipation, and thermodynamic limits of compute. This assumes near perfect engineering and huge scientific breakthroughs to get compute substrate that can reach these power efficiencies. Given a large amount of global initiative, GPT-9 () is likely to be the upper limit of training FLOP that is reachable without planet-scale major infrastructure projects and enormous scientific breakthroughs.
Footnotes
-
You could try to cover oceans too, for ~approximately a 3x gain, but you start to eat into the emissivity of earth. The 168 W / m number accounts for solar cycle and average over lattitudes. For example, well-oriented panels at the equator are about 270 W / m. ↩
-
I use 300K for these calculations, instead of 290K, because the cooling will be much more efficient with some kind of temperature gap between the place of compute and Earth's temperature. ↩
-
there is literally a top500 machine called Frontier that is 1.6 exaFlop ↩
-
For example, described here https://arxiv.org/abs/2312.11805 ↩
-
https://epochai.org/data/notable-ai-models, https://situational-awareness.ai/from-gpt-4-to-agi/ ↩