| designation: | D1-006 |
|---|---|
| author: | andrew white |
| status: | complete |
| prepared date: | December 1, 2024 |
| updated date: | December 1, 2024 |
abstract: Percentages are always thrown around in print or social media to make something more "scientific." I've always wondered if you can infer something about population size from the value - like does a percentage of 66% imply a larger population size than one of 67%? I show an argument below using some bibliometrics and Bayesian inference, that indeed you can infer something about population size from a reported percentage.
Predicting population size from percentage
Can you predict the population size from a percentage? For example, if you hear that 99% of dentists prefer something - at least 100 dentists had to be asked. If you consider rounding - then 67 is the smallest number of dentists that could be asked because 66/67 = 98.5%, which rounds to 99%. If 67% of dentists prefer public transit, the population size could have been 3 (2/3), 6 (4/6), etc. So there is some information about relationship between reported percentage and population size.
Let's take this to the extreme and see how accurate we can be at predicting population size form percentages.
The problem setting
Let's define a few items. The goal is to predict the population size from percentage - we want the probability of population size given the percentage we found. So we are after
where is population size and is a reported percentage. The underlying event space is a set of where is a numerator whose fraction is reported as a (possibly rounded) percentage. Note that we can convert from and to :
I'll make the following assumptions:
- (to make the problem tractable)
- Percentages are reported with no decimals (e.g., no )
You can easily relax these restrictions, but I think this is the most interesting setting.
Bayesian Formulation
It's actually pretty straightforward to work with because we can just enumerate the 's to see all possible values. For example, if , then we can only observe from . So , for example.
We will necessarily assume that whatever is being measured is irrelevant here for computing these probabilities. Obviously, this is not the case in general. Like we could take Benford's law1 for predicting distribution of the integers because we expect them to be occurring from real world measurements. But I think this will be a slight effect -- the more important effect is the support (zero value probabilities) rather than any slight shift of the non-zero probabilities.
OK, so let's write out the equation to get to :
where is the normalization constant. Now we need to come up with a prior for
The simplest prior is obviously . From our assumptions - . I'll call this prior
It is worth noting that does not imply a uniform . For to be uniform, it means that the same probability mass () is on each set of possible s. So, is much more probable than .
We can also try to measure by looking at published scientific literature. A quick method for this is to just do a google scholar search for "sample size of [X]" and look at result count. We'll call this .
Calculations
There is a way to do this analytically if there was no rounding. I'll leave it as an exercise for readers, but you can analytically compute using greatest common denominators/coprimes with some nice simple expressions by assuming because it cancels with definition of a percentage. However, all of this is useless once you consider rounding and it is not easy to do analytically.
So, we can just brute-force these calculations. It's easy enough - we just iterate over and and bin the rounded percentages. The main code is below:
Nmax = 100
pton = {p: [] for p in range(100 + 1)}
ntop = {n: [] for n in range(Nmax + 1)}
for N in range(1, Nmax + 1):
for a in range(N + 1):
p = round((a / N) * 100)
pton[p].append(N)
ntop[N].append(p)
def prob_percent(N):
ps = ntop[N]
counts, _ = np.histogram(ps, bins=np.arange(-0.5, 100.5 + 1, 1), density=True)
return counts
Results
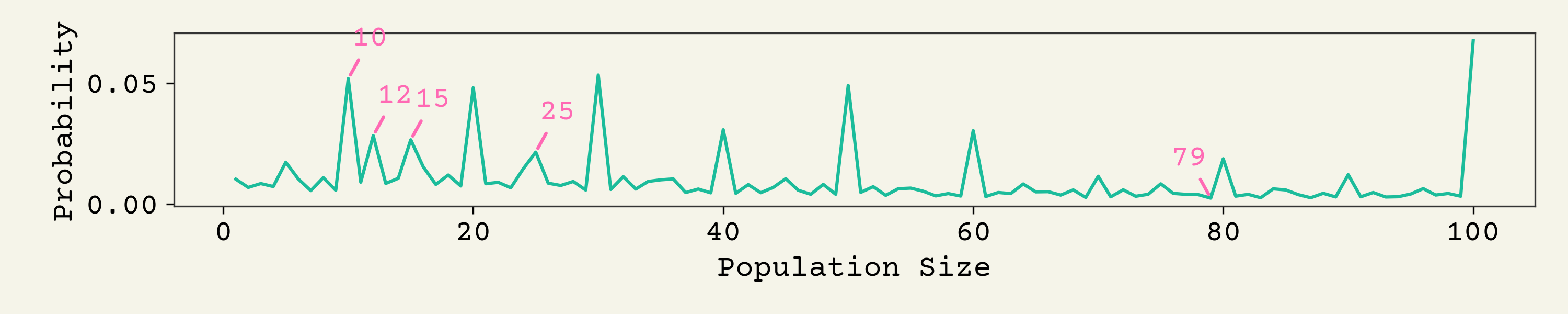
Let's start with the empirical prior, . Remember, I created this by just doing a bunch of google scholar searches of the form "sample size of [X]" and then normalize the number of results to sum to 1:
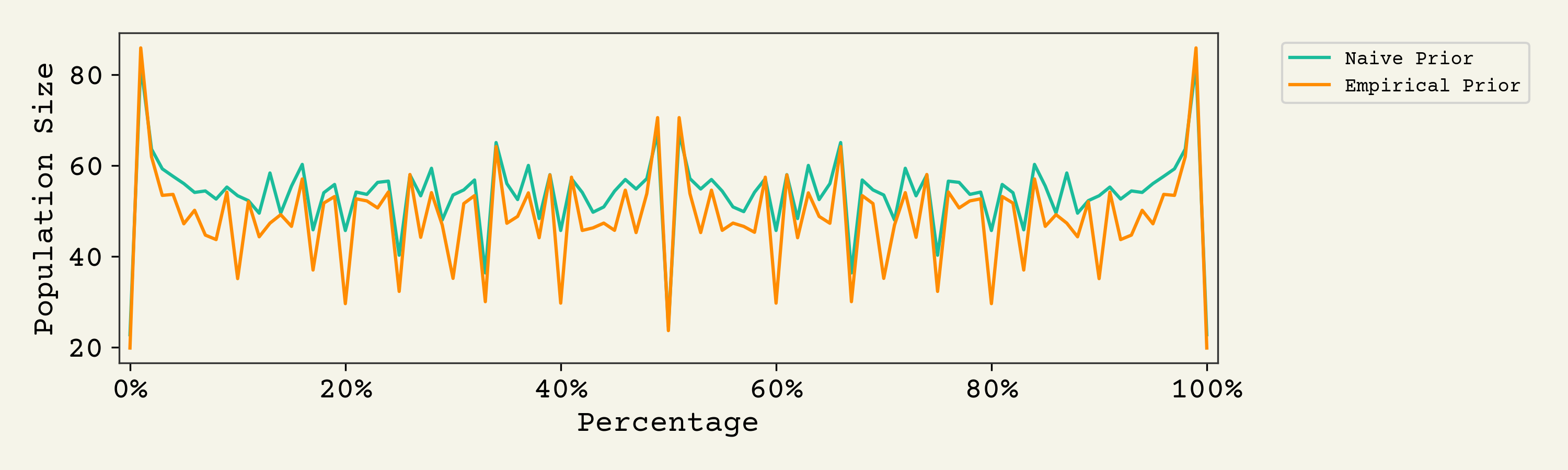
You can see that humans do not pick sample sizes randomly. The largest one, 100, I believe comes from statistical power recommendations in clinical trials. 100 is a common rule of thumb for early phase or pre-clinical trial designs. 10, 12, 15, 20, 30, 40, 50 are all popular population sizes. 25 is actually less common than I would have thought, since it's commonly quoted as a good rule of thumb for when the central limit applies. I guess 79 is the least popular population size.
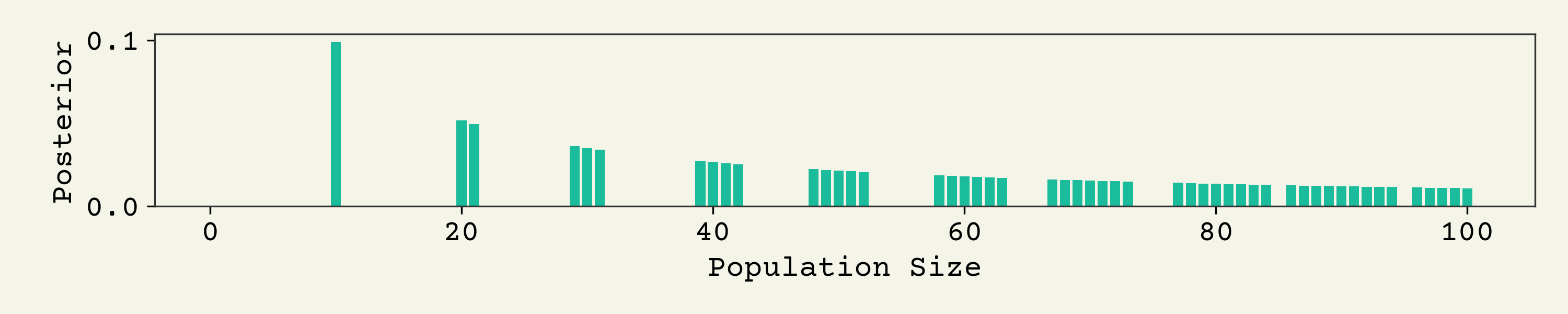
Now let's look at some specific posteriors. Starting with the naive prior, the posterior of 10% is shown below
You can see that a population of at least 10 is required. It kind of goes in multiples of 10 after that, as you might expect, but things spread out because of rounding. For example, 9 / 91, will still give 10%.
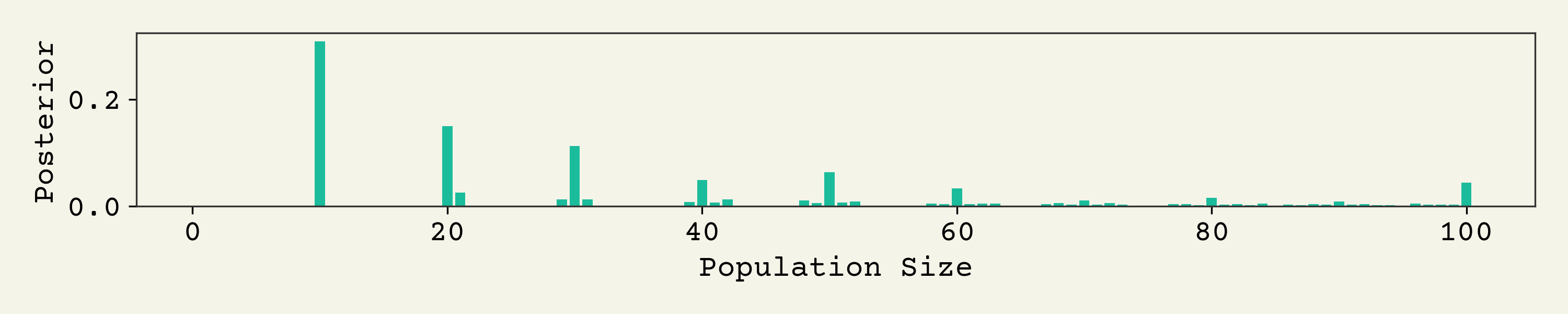
Now let's examine with the empirical prior distribution. Remember - we're looking at the probability that the population size was given that a percentage of some effect was reported at 10%.
Clearly there is a big effect because of the focus on multiples of 10 in the prior distribution. You can see that strong prior on 100 playing a role too.
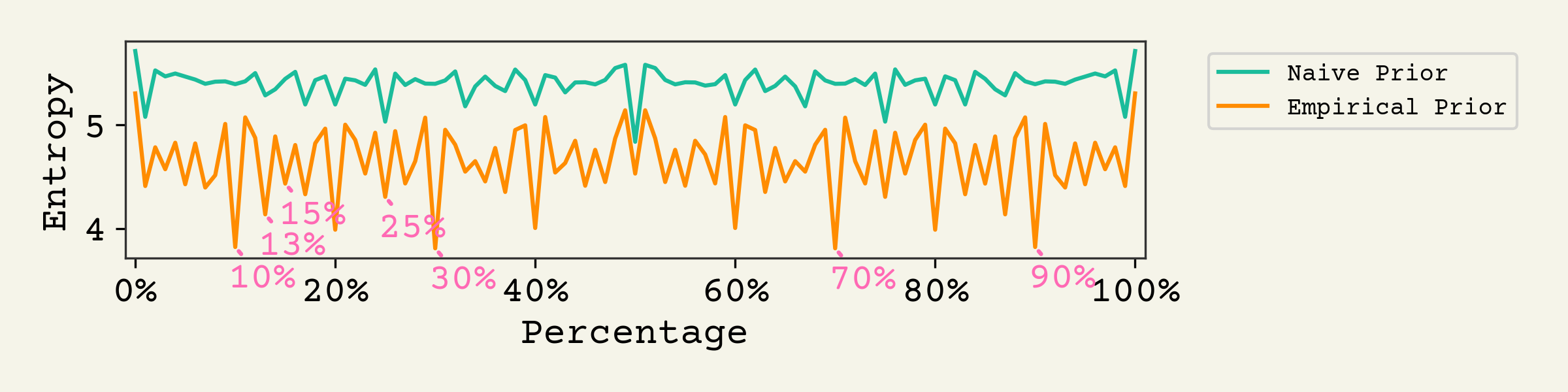
A natural question is how sharp are these distributions. Put another way, how much does our belief about the population size change for each observed percentage. This can be computed as entropy of the posterior, which is a single number of a distribution that measures how peaked/diffuse it is (higher entropy means more diffuse)2
There is clearly more entropy if we take , which is reasonable because of how strong that prior is. 50% is the lowest entropy under the naive prior. However, once you bring in the empirical prior - 10%, 13%, 30%, 70%, and 90% - are much lower than 50%.
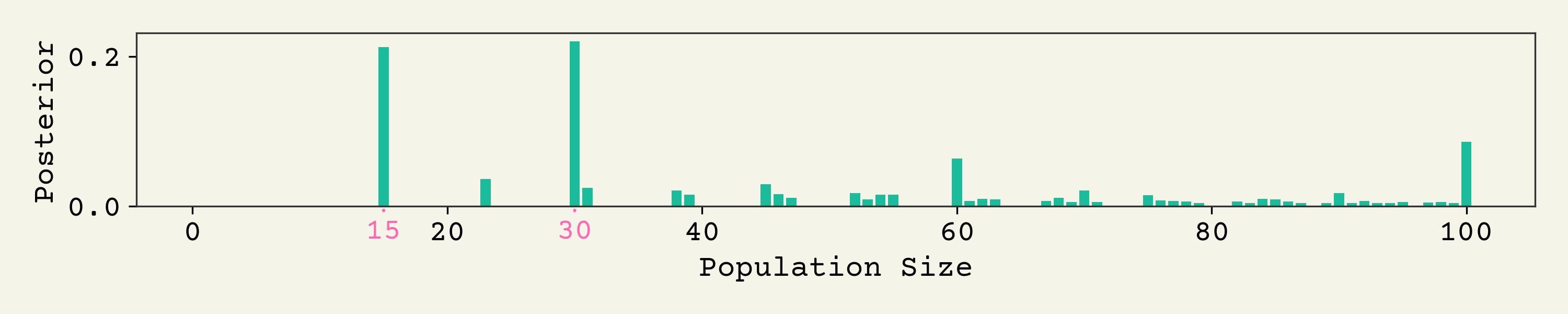
Let's look at one of these: 13%. Here is its posterior . What is probability that the population size was given that a percentage of some effect was reported at 13%.
There are two big peaks - at 15 and 30. This is a sharp, low entropy distribution. Why 15 and 30? These come from , which rounds to 13%. Also, 15 and 30 have strong priors.
A reason to do this analysis is to see if a specific percentage indicates a study is underpowered. For example, if I see 33% reported in a newspaper, I'm always suspicious they asked three people. So let's just compute the expected population size from these posteriors:
Now we can convert this into a handy table of suspicious percentages and their corresponding posterior mean population sizes:
| Percentage | Posterior Expected Population |
|---|---|
| 0% | 19.9 |
| 100% | 19.9 |
| 50% | 23.7 |
| 20% | 29.7 |
| 80% | 29.7 |
| 40% | 29.8 |
| 60% | 29.8 |
| 33% | 30.1 |
| 67% | 30.1 |
| 75% | 32.3 |
| 25% | 32.3 |
| 10% | 35.2 |
| 90% | 35.2 |
| 70% | 35.2 |
| 30% | 35.2 |
| 17% | 37.0 |
| 83% | 37.0 |
| 92% | 43.7 |
| 8% | 43.7 |
Magic Trick
Ok, now let's see if you can actually predict population sizes from the percentage. For example, if you see a percentage of 63%, then predicting a population size of 30 will be correct 1/4 of the time. So if at a party someone says "did you know 63% of millenials own dogecoin", then you can say that they probably only asked 30 people. And you'd probably be wrong. So actually I'm not sure what to do with this information. Anyway, here you go: the most predictable population sizes from a reported percentage.
| Max Prob | Percentage | Likely |
|---|---|---|
| 0.311 | 30% | 10 |
| 0.311 | 70% | 10 |
| 0.309 | 10% | 10 |
| 0.309 | 90% | 10 |
| 0.267 | 37% | 30 |
| 0.267 | 63% | 30 |
| 0.267 | 5% | 20 |
| 0.267 | 95% | 20 |
| 0.264 | 35% | 20 |
| 0.264 | 65% | 20 |
| 0.261 | 15% | 20 |
| 0.261 | 85% | 20 |
| 0.258 | 45% | 20 |
| 0.258 | 55% | 20 |
| 0.248 | 1% | 100 |
| 0.248 | 99% | 100 |
Conclusion
As I proposed in the abstract, 66% is a great percentage. It has a posterior mean population size of 64.2, whereas 67% is 30.1. So there really is something more "trustworthy" about some percentages vs others.
Footnotes
-
You could go fancier here and consider starting entropy in the prior, but let's just keep it simple. ↩